H3:Uber的六边型层次空间索引
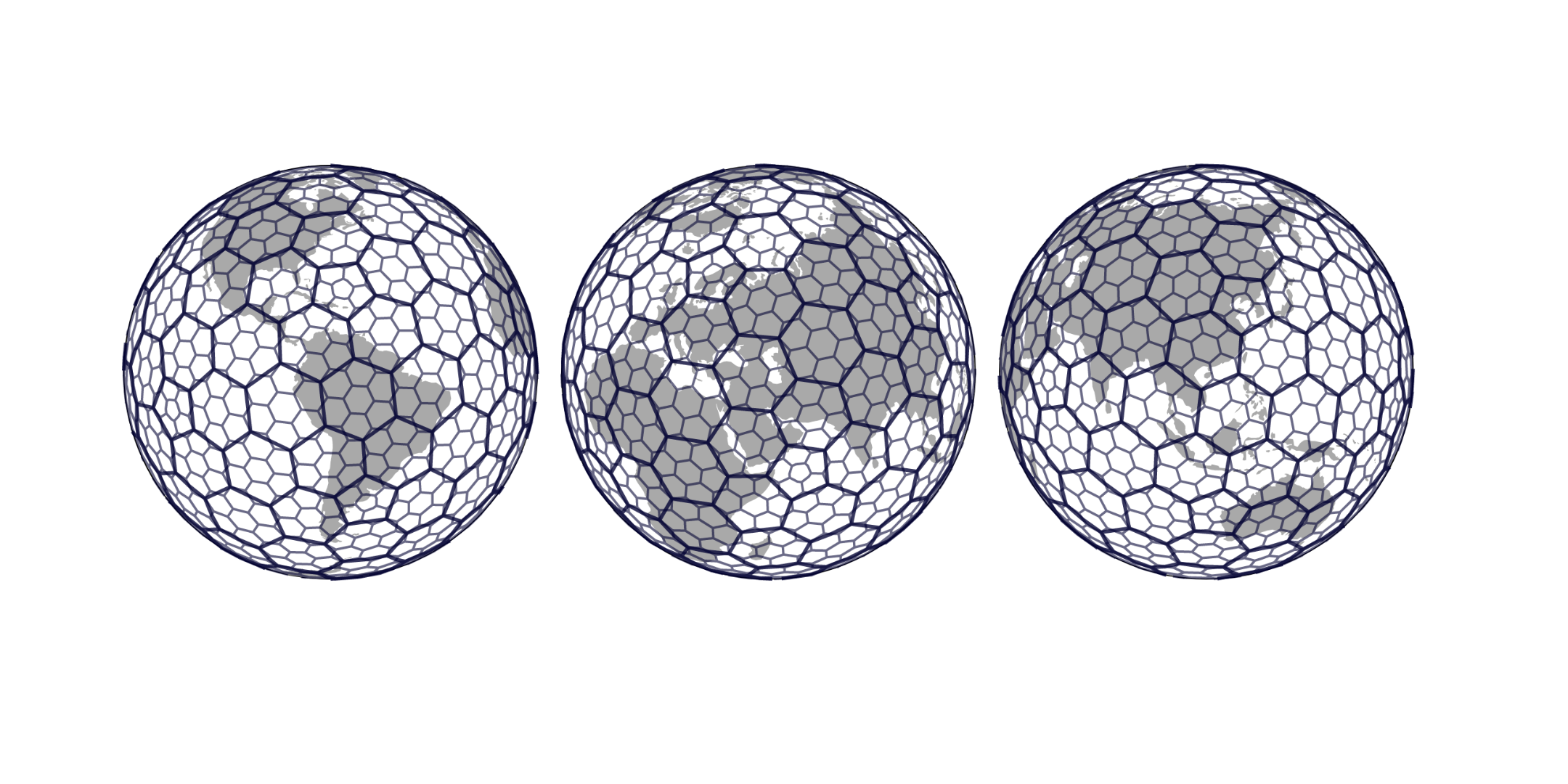 网格系统(Grid System)对于分析海量空间数据集,将地球空间划分为可识别的网格单元(cell)至关重要。
网格系统(Grid System)对于分析海量空间数据集,将地球空间划分为可识别的网格单元(cell)至关重要。
考虑到这一点,Uber开发了 H3 ,这是我们的网格系统,它可以用来有效优化乘车价格和调度、地图空间数据的可视化和挖掘。 H3使我们能够分析地理信息以设置动态价格并在整个城市范围内做出决策。 我们将H3作为网格系统用于整个市场的分析和优化。 H3就是为此目的而设计的,它使我们可以使用六边形层次索引。
今年早些时候,我们在Github上 开源了H3 ,大家都可以使用此强大的解决方案,上周,我们开源了 H3 JavaScript 版本。 在本文中,我们讨论了为什么我们使用网格系统,H3的某些独特属性以及如何开始使用H3。
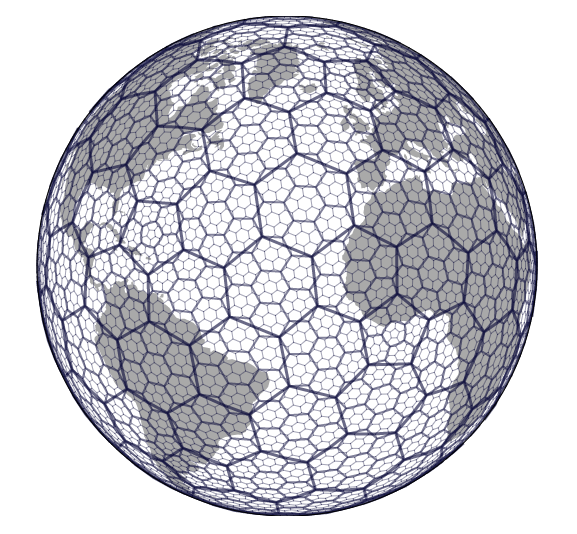
图1. H3把地球分成很多六边形,使用户可以进行更精准的分析。
使用网格进行分析
每天,Uber市场都会发生数以百万计数的事件。时时刻刻, 平台上的这些事件都在产生,包括但不限于:乘客请求乘车、驾驶员搭伴出行,饿了的用户寻找食物。 每个事件都发生在特定的位置,例如,乘客在自己家中发起乘车订单,而驾驶员则在几英里外的汽车中接受该订单。
这些事件使Uber能够更好地了解和优化我们的服务。 例如,这些事件可能告诉我们在城市的某个地方需求大于供应,然后我们就可以做出相应的价格调整,或者通知平台的某个Uber驾驶员附近有两个乘车订单。
要从Uber业务数据中获取信息和知识,需要分析整个城市的数据。 由于城市在地理位置上是多种多样的,因此需要以精细的粒度进行分析。 以精细的粒度(事件发生的确切位置)进行分析是非常困难且费力的。 对区域(例如城市中的社区)进行分析更加切实可行。
 |
 |
 |
|---|---|---|
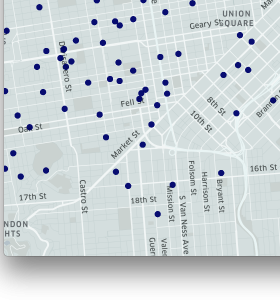
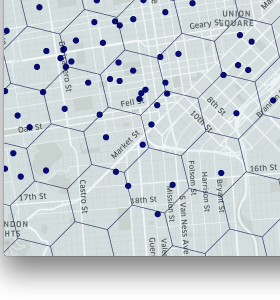
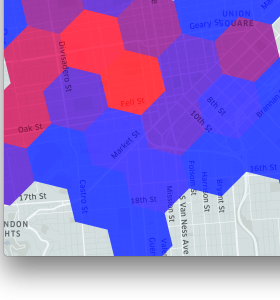
| 汽车分布在城市 | 汽车分割到六边形 | 六边形内汽车数量热度 |
| 图2.上面的地图描绘了使用H3进行分割的过程 |
我们使用网格系统将事件存储到六边形区域(即单元格)中。 数据点存储在六边形中,可以使用六边形存储的数据来标识。 例如,我们通过测量所服务的每个城市中六边形的供求来计算高峰价格。 这些六边形构成了我们分析Uber业务的基础。
六边形是一个重要的选择,因为城市中的人们经常在运动,而六边形可以最大程度地减少用户穿越城市时引入的 量化误差 。 六边形还使我们可以轻松地获取近似半径,例如在 此示例中使用Elasticsearch 。
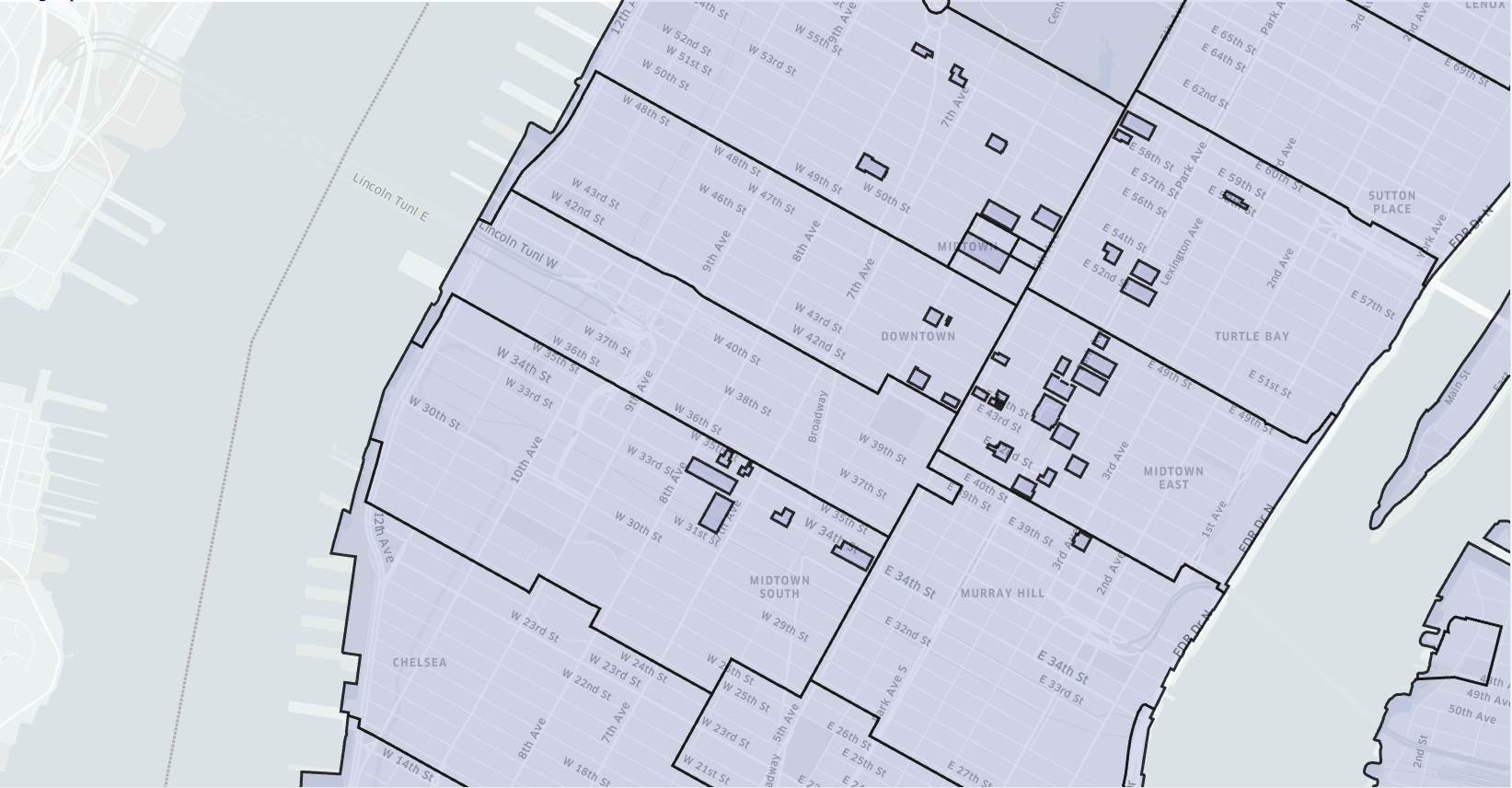
图3.纽约市(曼哈顿)的邮政编码地图
当然,我们也可以使用其他的方案把事件存储到区域中,例如多边形区域。 这些区域可能是邮政编码标识的区域,但是这些区域具有不规则的形状和大小,对分析没有帮助,并且区域划分随时发生改变,而这些改变与我们使用它们的目的 完全无关的 。 Uber运营团队还可以根据他们对城市的了解来划定区域,但是随着城市的变化,这些区域需要经常更新,并且经常随意定义区域的边缘。
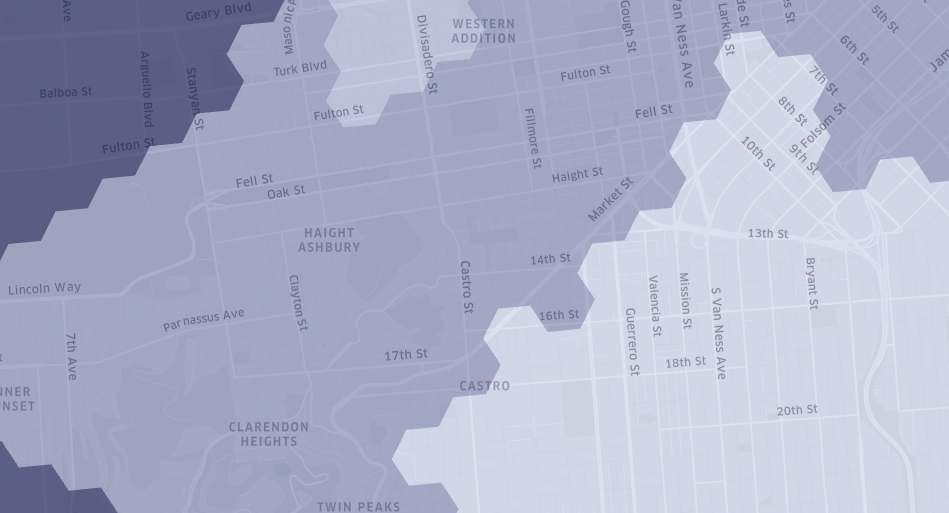
图4.随机生成的六边形簇覆盖旧金山市
网格系统在Uber运营所在的城市中应该具有可比的形状和大小,并且不受任意更改。 尽管网格系统无法与城市中的街道和社区保持一致,但可以通过对网格单元进行聚合来将其有效地表示社区。 可以使用目标函数完成聚合,从而生成对分析更有用的形状。 确定聚类的成员与设置查找操作也应该是很高效的。
H3
我们决定创建H3,以充分利用到六边形全局网格系统这一层次索引系统。
全球网格系统通常至少需要两件事:地图投影和放置在地图上的网格。 从地球上的三维位置到地图上的二维点需要地图投影。 然后将网格覆盖在地图上,形成一个全球网格系统。
通过组合不同的地图投影和网格(例如,广为人知的墨卡托投影 和正方形网格),可以无数种方式完成此过程 。 尽管此简单方法行之有效,但它有许多缺点。 首先,墨卡托投影的大小会明显失真,因此某些网格的面积会大不相同。 正方形也有缺点,在用于分析时需要多组系数。 这个缺点是正方形具有两种不同类型的邻居的结果,一种邻居共享它们的边(在4个基本方向上),另一种邻居共享顶点(在4个对角线上)。
 |
 |
 |
|---|---|---|
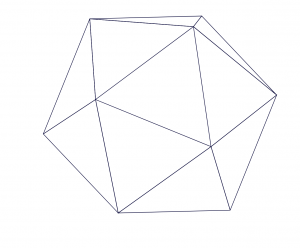
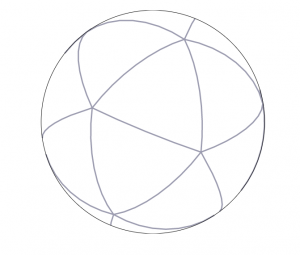
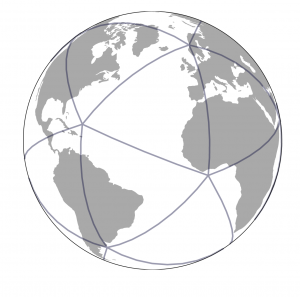
| 正二十面体 | 球形二十面体 |
图5.我们选择使用以正二十面体(左)为中心的球心投影进行H3的地图投影,将地球投影为球形二十面体(右)
对于地图投影,我们选择使用以 正二十面体 的面为中心的球心投影 。 它从地球作为一个球体投射到二十面体的二十个面。 基于二十面体的地图投影会产生二十个单独的二维平面,而不是单个平面。 每次,生成一个二维映射地图,正二十面体可以有 多种方式展开 。 但是,H3不会展开正二十面体以构建其网格系统,而是将其网格放置在二十面体的面自身上,从而形成了 测地线全球离散网格系统 。
 |
 |
 |
|---|---|---|
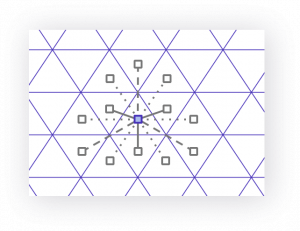
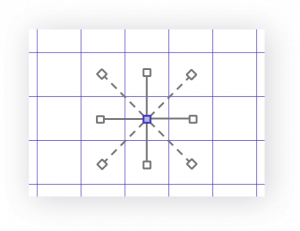
| 三角形到其邻居的距离 | 正方形到其邻居的距离 | 六边形到其邻居的距离 |
图6.三角形,正方形,六边形到其邻居的距离
使用六边形作为单元格形状对于H3至关重要。 如图6所示,与正方形的2个距离或三角形的3个距离相比,六角形在中心点与其相邻点之间只有一个距离。 此属性极大地简化了梯度的分析和平滑处理。
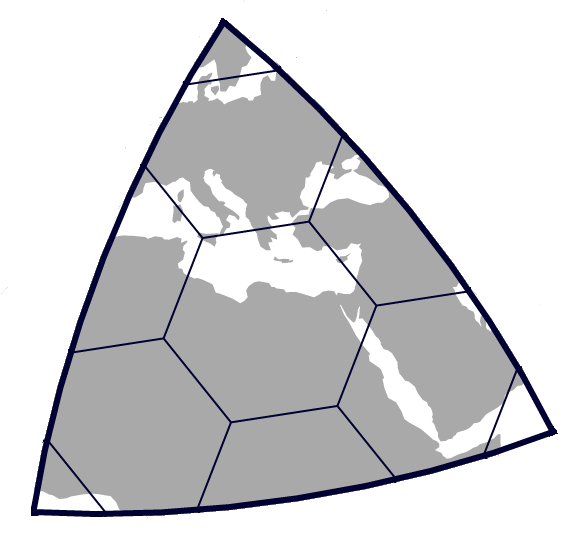
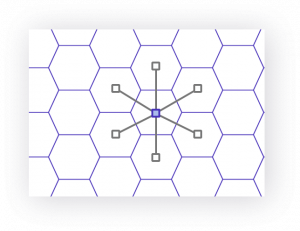
图7.用于在单个正二十面体的面上创建网格的H3。
H3网格是通过在地球上布置122个基本单元构成的,每个面有10个单元。 有些单元格跨越多个面。 由于不可能仅用六边形平铺二十面体,因此我们选择引入12个五边形,每个二十面体顶点分别一个。 这些顶点是使用 R. Buckminster Fuller 的球形二十面体方向进行定位的 ,它将所有顶点都放置在大海中。 这有助于避免五边形出现在我们的陆地上,从而不会对实际工作产生影响。
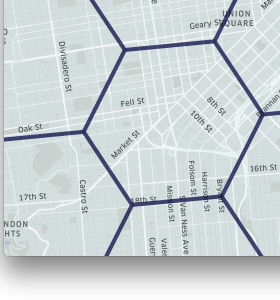 |
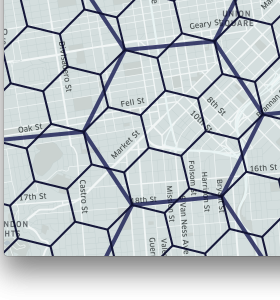 |
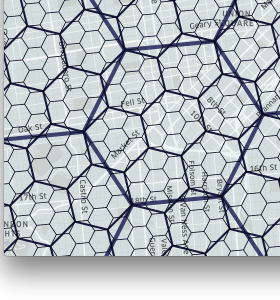 |
|---|---|---|
图8. H3使用户可以将区域细分为越来越小的六边形。
H3支持16种分辨率(resolution)。 每个较精细的分辨率所具有的单元的面积均为较粗糙分辨率的1/7。 六边形不能完美地细分为7个六边形,因此,较细的单元仅近似包含在父单元中。
这些子单元的标识符可以很容易地通过截断来快速的找到较粗分辨率的父单元,从而实现高效索引。 由于子单元格仅仅是近似包含,因此在截断过程会产生一定的形状失真。 不过只有当单元标识符截断时才会出现这种失真。 当以特定分辨率索引位置时,单元格边界是精确的。
H3入门
H3索引系统 是开源的,可在GitHub上获得。 H3库 本身是用C编写的,并且有多种语言的移植版本。 建议从各种移植版来开始使用H3。 Uber已经发布了 Java 和 JavaScript 版本 ,而社区已经为 更多语言 提供出来 。 Python和Go的版本即将推出。
 |
 |
 |
|---|---|---|
| 点(蓝色)在六边形内 | 六边形中心点(浅蓝色) | 六边形点和中心点 |
图9. 实际点与六边形中心点之间可能存在的差异
代码: https//github.com/uber/h3/blob/master/examples/index.c
H3库的基本功能是用于位置索引,该位置将纬度和经度对转换为 64位H3索引 ,用来识别网格单元。 函数 geoToH3 接受纬度,经度和分辨率(介于0和15之间,其中0是最粗的,15是最细的),并返回一个索引。 h3ToGeo 和 h3ToGeoBoundary 是此函数的逆函数,分别提供了由H3索引指定的网格单元的中心坐标和轮廓。
使用H3为数据建立索引后,H3 API将具有处理索引的功能。
 |
 |
 |
|---|---|---|
| 原始索引,距离0 | 原始索引的邻居,距离1 | 邻居的邻居,距离2 |
图10.六边形索引的邻居,距离为0,距离1和距离2(右;与邻居的邻居)
代码: https//github.com/uber/h3/blob/master/examples/neighbors.c
相邻的六边形具有使用网格系统近似圆行的特性。 kRing 函数提供原始索引的网格距离 k 内的网格单元 。
 |
 |
|---|---|
图11.加利福尼亚州:密集六边形与紧凑型六边形形成鲜明对比,只需要更少的六边形就可以表示同一个区域。
代码: https://github.com/uber/h3/blob/master/examples/compact.c
H3的层次结构性质使得可以高效地截断索引的精度(或分辨率)以及恢复原始索引。 上面显示了一组六边形的不紧凑和紧凑 表示。 非紧凑(uncompact)在分辨率6有10,633个六边形,而紧凑(compact)形式在最高为6的分辨率情况下只需要901个六边形。在两种情况下,六边形索引都是64位整数。
单个索引的精度可以按使用位运算被有效地截取缩小,或者扩展为更高精度的索引集。
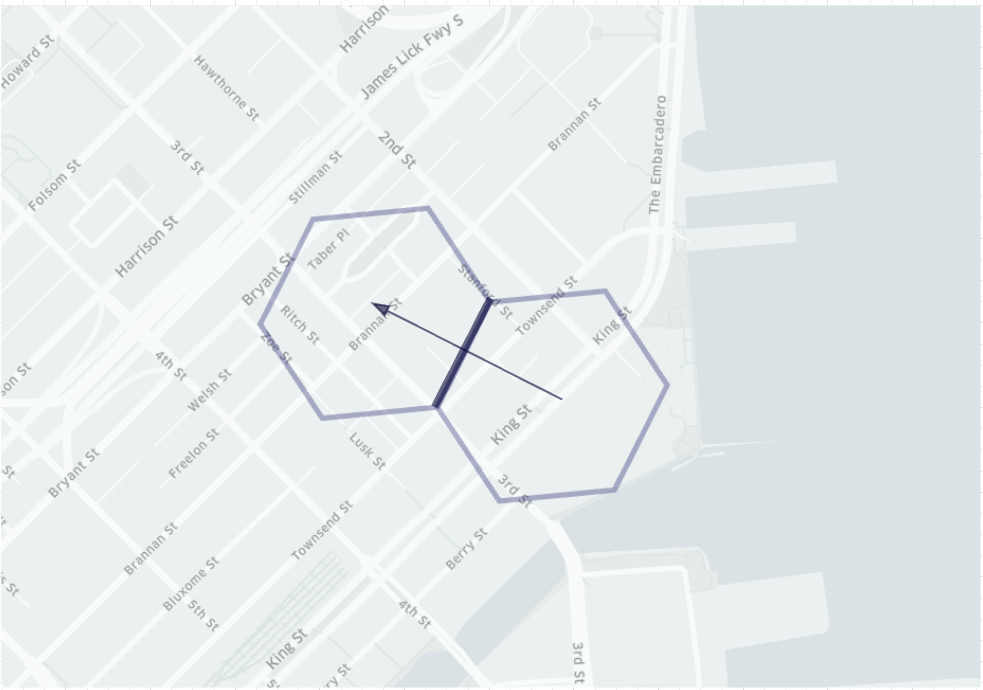
图12. H3可以表示从一个单元格到另一个单元格的移动,此处通过绘制从起点到目标单元格的箭头表示
代码: https://github.com/uber/h3/blob/master/examples/edge.c
H3具有 网格单元的有向边功能 ,可以表示从一个单元格到另一个单元格的运动。 有向边也存储为64位整数,可以从两个相邻的单元格中获取,也可以通过找到一个单元格的所有边来获得。 如果需要,可以将边线转换回原始索引或目标索引。
未来
H3在整个Uber中用于支持对我们市场的定量分析,并且由于它是开源的,您也可以免费试用! 我们期待您Fllow 在Github上的 存储库 并使用 #uberH3 主题标签发布推文,加入H3社区 。
翻译自: